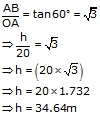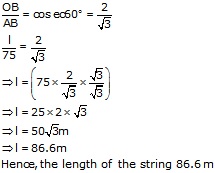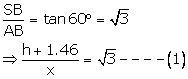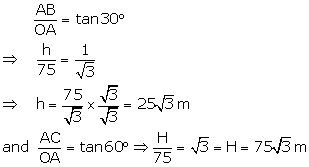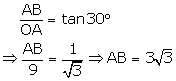RS Aggarwal Solutions for Class 10 Maths Chapter 14 Height and Distance: Subject matter experts have designed easy-to-understand solutions for RS Aggarwal Solutions for Class 10 Maths Chapter 14 Height and Distance. You can easily clear your doubts with this ultimate help guide. All the solutions of RS Aggarwal Solutions Class 10 Maths Chapter 14 are as per the current CBSE Syllabus.
You can download the RS Aggarwal Solutions Class 10 Maths Chapter 14 Height and Distance PDF for free from this blog.
Download the Free PDF Of RS Aggarwal Solutions for Class 10 Maths Chapter 14 Height and Distance
RS Aggarwal Solutions for Class 10 Maths Chapter 14 Height and Distance
Access The RS Aggarwal Class 8 Maths Chapter 23 Ex 23.1 Solutions
Solution 1
Let AB be the tower standing on a level ground and O be the position of the observer. Then OA = 20 m and OAB = 90° and
AOB = 60°
Let AB = h meters
From the right OAB, we have
Hence the height of the tower is
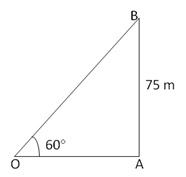
Solution 2
Let OB be the length of the string from the level of ground and O be the point of the observer, then, AB = 75m and OAB = 90° and
AOB = 60°, let OB = l meters.
From the right OAB, we have
Solution 3
Solution 4
Solution 5
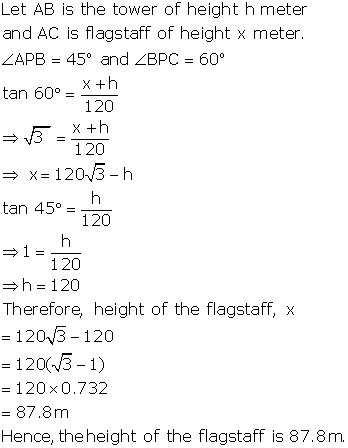
Solution 6

Solution 7
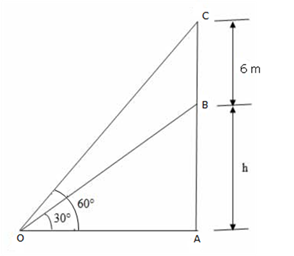
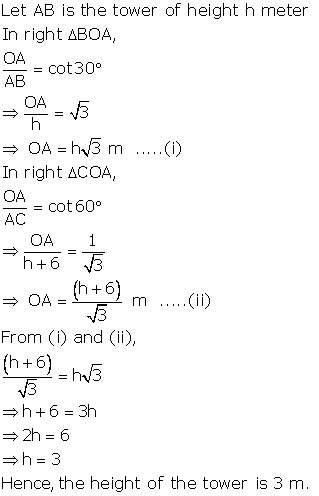
Solution 8
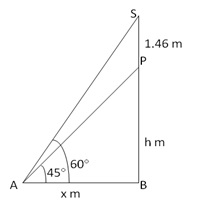
Let SP be the statue and PB be the pedestal. Angles of elevation of S and P are 60° and 45° respectively.
Further suppose AB = x m, PB = h m
In right ABS,
In right PAB,
Thus, height of the pedestal = 2m
Solution 9
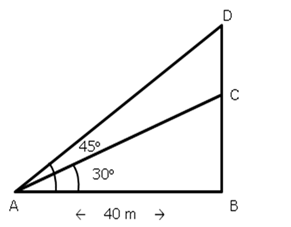
Let AB be the unfinished tower and let AC be complete tower.
Let O be the point of observation. Then,
OA = 75 m
AOB = 30° and
AOC = 60°
Let AB = h meters
And AC = H meters
Hence, the required height is
Solution 10
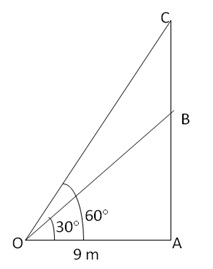
Let AB be the tower and BC be flagpole, Let O be the point of observation.
Then, OA = 9 m, AOB = 30° and
AOC = 60°
From right angled BOA
From right angled OAC
Thus
Hence, height of the tower= 5.196 m and the height of the flagpole = 10.392 m
RS Aggarwal Solutions for Class 10 Maths Chapter 14 Height and Distance – Overview
Chapter 14 of RS Aggarwal Solutions Class 10 Maths comes with one exercise and all the questions related to the topic of Height and Distance.
All the topics are very well-explained in RS Aggarwal Solutions Class 10 Maths Chapter 14. The questions are explained in a step-by-step manner and are very accurate. To clear your doubts in detail, this is the perfect guide for you.
Class 10 RS Aggarwal Solutions – Height and Distances
In this chapter, we will learn how to solve questions related to the heights of the rectangular prism and the rectangular trapezoid using Pythagoras’ theorem. Both the prisms and trapezoids are considered rectangular in this chapter, which means they are rectangles or rectangle-shaped solids. They are made of right rectangularly aligned rows of points of various lengths
Pythagoras’ Theorem:
The height of a triangle is given by the Area of the triangle: c . h . d
Where
c = the length of the hypotenuse
d = the length of the leg
h = the height of the triangle.
Access RS Aggarwal Solutions Class 10 Maths Chapter 14 Other Important Exercises
RS Aggarwal Solutions Chapter 14 Exercise 14.1
This is the complete blog on the RS Aggarwal Solutions Class 10 Maths Chapter 14. To know more about the CBSE Class 10 Maths exam, ask in the comments.
FAQs on RS Aggarwal Solutions Class 10 Maths Chapter 14
From where can I find the download link for the RS Aggarwal Solutions Class 10 Maths Chapter 14 PDF?
You can find the download link of the RS Aggarwal Solutions Class 10 Maths Chapter 14 PDF in the above blog.
How much does it cost to download the RS Aggarwal Solutions Class 10 Maths Chapter 14 PDF?
You can download RS Aggarwal Solutions Class 10 Maths Chapter 14 PDF for free.
Can I access the RS Aggarwal Solutions Class 10 Maths Chapter 14 PDF offline?
Once you have downloaded the RS Aggarwal Solutions Class 10 Maths Chapter 14 PDF online, you can access it offline whenever you want.