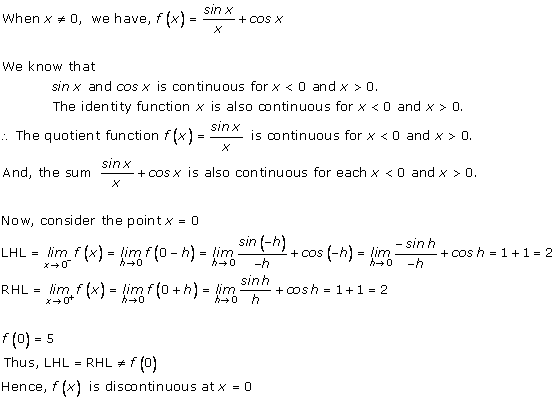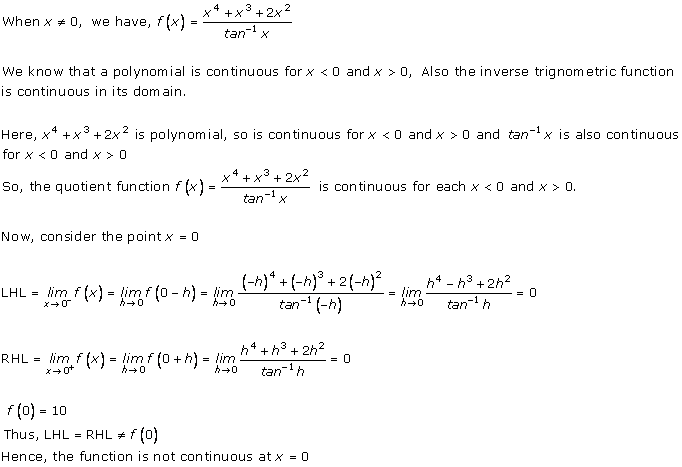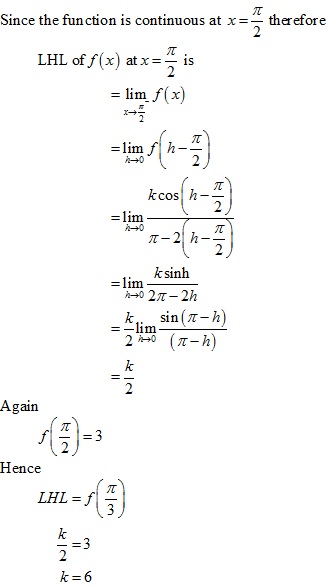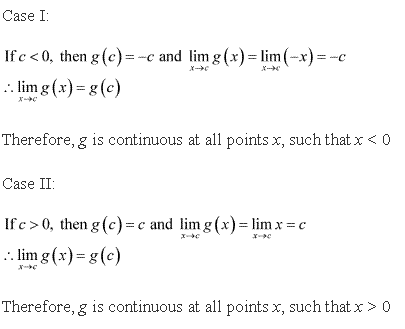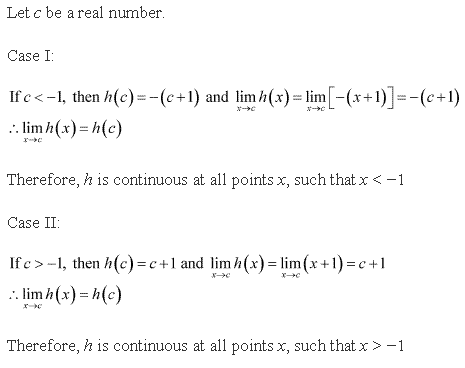RD Sharma Solutions Class 12 Maths Chapter 9 Exercise 9.2: This exercise is primarily concerned with continuity on a particular function’s interval. Kopykitab’s subject experts with extensive knowledge of subjects provide solutions that are tailored to the students’ understanding abilities. Here you will find RD Sharma Solutions for Class 12 Maths Chapter 9 Continuity Exercise 9.2.
Download RD Sharma Solutions Class 12 Maths Chapter 9 Exercise 9.2 Free PDF
RD Sharma Solutions Class 12 Maths Chapter 9 Exercise 9.2
Access answers to Maths RD Sharma Solutions For Class 12 Chapter 9 – Continuity Exercise 9.2 Important Questions With Solution

Solution:
A real function f is said to be continuous at x = c, where c is any point in the domain of f if

Where h is a very small positive number. i.e. left hand limit as x → c (LHL) = right hand limit as x → c (RHL) = value of function at x = c.
A function is continuous at x = c if

To prove it everywhere continuous we need to show that at every point in the domain of f(x) [domain is nothing but a set of real numbers for which function is defined]

Clearly from definition of f(x), f(x) is defined for all real numbers.
Now we need to check the continuity for all real numbers.
Let c is any random number such that c < 0 [thus c being a random number, it can include all negative numbers]

We can say that f(x) is continuous for all x < 0
Now, let m be any random number from the domain of f such that m > 0
Thus m being a random number, it can include all positive numbers]

Therefore we can say that f(x) is continuous for all x > 0
As zero is a point at which function is changing its nature so we need to check LHL, RHL separately
f (0) = 0 + 1 = 1 [using equation 1]

Thus LHL = RHL = f (0).
Therefore f (x) is continuous at x = 0
Hence, we proved that f is continuous for x < 0; x > 0 and x = 0
Thus f(x) is continuous everywhere.
Hence, proved.

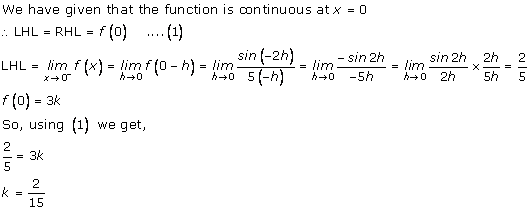
Solution:
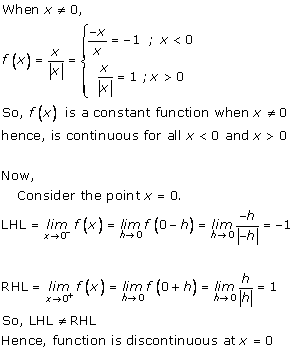
3. Find the points of discontinuity, if any, of the following functions:

Solution:

Solution:

Solution:
Chapter 9 Continuity Ex 9.2 Q3(iv)
Chapter 9 Continuity Ex 9.2 Q3(v)
Chapter 9 Continuity Ex 9.2 Q3(vi)
Chapter 9 Continuity Ex 9.2 Q3(vii)
Chapter 9 Continuity Ex 9.2 Q3(viii)
Chapter 9 Continuity Ex 9.2 Q3(ix)
Chapter 9 Continuity Ex 9.2 Q3(xi)
Chapter 9 Continuity Ex 9.2 Q3(xii)
Chapter 9 Continuity Ex 9.2 Q3(xiii)
Chapter 9 Continuity Ex 9.2 Q4(i)
Chapter 9 Continuity Ex 9.2 Q4(ii)
Chapter 9 Continuity Ex 9.2 Q4(iii)
Chapter 9 Continuity Ex 9.2 Q4(iv)
Chapter 9 Continuity Ex 9.2 Q4(v)
Chapter 9 Continuity Ex 9.2 Q4(vi)
Chapter 9 Continuity Ex 9.2 Q4(vii)
Chapter 9 Continuity Ex 9.2 Q4(viii)
Chapter 9 Continuity Ex 9.2 Q5
Chapter 9 Continuity Ex 9.2 Q6
Chapter 9 Continuity Ex 9.2 Q7
Chapter 9 Continuity Ex 9.2 Q8
Chapter 9 Continuity Ex 9.2 Q9
Chapter 9 Continuity Ex 9.2 Q10
Chapter 9 Continuity Ex 9.2 Q11
Chapter 9 Continuity Ex 9.2 Q12
Chapter 9 Continuity Ex 9.2 Q13
Chapter 9 Continuity Ex 9.2 Q14
Chapter 9 Continuity Ex 9.2 Q15
Chapter 9 Continuity Ex 9.2 Q16
Chapter 9 Continuity Ex 9.2 Q17
Chapter 9 Continuity Ex 9.2 Q18
Chapter 9 Continuity Ex 9.2 Q19
RD Sharma Class 12 Solutions Chapter 9 Exercise 9.2 | Important Concepts
Let’s have a look at some of the concepts covered in RD Sharma Class 12 Solutions Chapter 9 Exercise 9.2:
- Continuity on an interval
- Continuity on an open interval
- Continuity on a closed interval
- Definition and meaning of continuous function
- Definition and meaning of everywhere continuous function
- Properties of a continuous function
- Testing the continuity of a function in its domain
- Finding the values of a constant given in the definition of a function when it is continuous on its domain
We have provided complete details of RD Sharma Solutions Class 12 Maths Chapter 9 Exercise 9.2. If you have any queries related to CBSE, feel free to ask us in the comment section below.
FAQs on RD Sharma Solutions Class 12 Maths Chapter 9 Exercise 9.2
How can students use the RD Sharma Solutions Class 12 Maths Chapter 9 Exercise 9.2 to prepare for the annual exam?
To gain a clear understanding of the key concepts, students must thoroughly study the chapter and practice all of the exercise questions. Kopykitab’s expert subject teachers created the RD Sharma Solutions, which are an excellent resource for exam preparation. While addressing the RD Sharma questions, students can refer to these solutions to clear up any misconceptions and achieve a good rank.
Where can I get RD Sharma Class 12 Maths Solutions Chapter 9 Exercise 9.2 Free PDF?
You can get RD Sharma Solutions Class 12 Maths Chapter 9 Exercise 9.2 Free PDF from the above article.
How many questions are there in RD Sharma Solutions Class 12 Maths Chapter 9 Exercise 9.2?
There are a total of 19 questions in RD Sharma Solutions Class 12 Maths Chapter 9 Exercise 9.2.