RD Sharma Class 12 Solutions Chapter 6 Determinants Exercise 6.1 (Updated for 2024)

RD Sharma Solutions Class 12 Maths Chapter 6 Exercise 6.1: The key topics covered in exercise 6.1 are the determinant of a square matrix of order 1, 2, 3, and 4, singular matrix, minors, and cofactors of specified determinants. Students can use this exercise as a model of reference to strengthen their conceptual knowledge and comprehend the various methods utilized to solve problems. RD Sharma Solutions Class 12 Maths Chapter 6 Exercise 6.1 is available in PDF format. The RD Sharma Class 12 Solutions were designed by Kopykitab’s Math experts in order to boost students’ confidence, which is important in board exams.

Download RD Sharma Solutions Class 12 Maths Chapter 6 Exercise 6.1 Free PDF

RD Sharma Solutions Class 12 Maths Chapter 6 Exercise 6.1

Access answers to Maths RD Sharma Solutions For Class 12 Chapter 6 – Determinants Exercise 6.1 Important Questions With Solution

1. Write the minors and cofactors of each element of the first column of the following matrices and hence evaluate the determinant in each case:

Solution:

(i) Let M_ij and C_ij represent the minor and cofactor of an element, where i and j represent the row and column. The minor of the matrix can be obtained for a particular element by removing the row and column where the element is present. Then find the absolute value of the matrix newly formed.

Also, C_ij = (–1)^i+j × M_ij

Given,

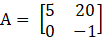
From the given matrix we have,

M₁₁ = –1

M₂₁ = 20

C₁₁ = (–1)¹⁺¹ × M₁₁

= 1 × –1

= –1

C₂₁ = (–1)²⁺¹ × M₂₁

= 20 × –1

= –20

Now expanding along the first column we get

|A| = a₁₁ × C₁₁ + a₂₁× C₂₁

= 5× (–1) + 0 × (–20)

= –5

(ii) Let M_ij and C_ij represent the minor and co–factor of an element, where i and j represent the row and column. The minor of matrix can be obtained for particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.

Also, C_ij = (–1)^i+j × M_ij

Given

From the above matrix we have

M₁₁ = 3

M₂₁ = 4

C₁₁ = (–1)¹⁺¹ × M₁₁

= 1 × 3

= 3

C₂₁ = (–1)²⁺¹ × 4

= –1 × 4

= –4

Now expanding along the first column we get

|A| = a₁₁ × C₁₁ + a₂₁× C₂₁

= –1× 3 + 2 × (–4)

= –11

(iii) Let M_ij and C_ij represents the minor and co–factor of an element, where i and j represent the row and column. The minor of the matrix can be obtained for a particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.

Also, C_ij = (–1)^i+j × M_ij

Given,

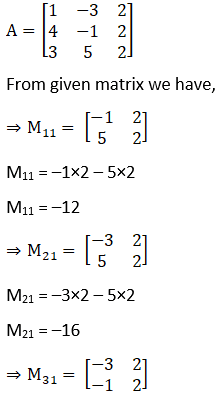
M₃₁ = –3 × 2 – (–1) × 2

M₃₁ = –4

C₁₁ = (–1)¹⁺¹ × M₁₁

= 1 × –12

= –12

C₂₁ = (–1)²⁺¹ × M₂₁

= –1 × –16

= 16

C₃₁ = (–1)³⁺¹ × M₃₁

= 1 × –4

= –4

Now expanding along the first column we get

|A| = a₁₁ × C₁₁ + a₂₁× C₂₁+ a₃₁× C₃₁

= 1× (–12) + 4 × 16 + 3× (–4)

= –12 + 64 –12

= 40

(iv) Let M_ij and C_ij represents the minor and co–factor of an element, where i and j represent the row and column. The minor of the matrix can be obtained for a particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.

Also, C_ij = (–1)^i+j × M_ij

Given,

M₃₁ = a × c a – b × bc

M₃₁ = a²c – b²c

C₁₁ = (–1)¹⁺¹ × M₁₁

= 1 × (ab² – ac²)

= ab² – ac²

C₂₁ = (–1)²⁺¹ × M₂₁

= –1 × (a²b – c²b)

= c²b – a²b

C₃₁ = (–1)³⁺¹ × M₃₁

= 1 × (a²c – b²c)

= a²c – b²c

Now expanding along the first column we get

|A| = a₁₁ × C₁₁ + a₂₁× C₂₁+ a₃₁× C₃₁

= 1× (ab² – ac²) + 1 × (c²b – a²b) + 1× (a²c – b²c)

= ab² – ac² + c²b – a²b + a²c – b²c

(v) Let M_ij and C_ij represents the minor and co–factor of an element, where i and j represent the row and column. The minor of matrix can be obtained for particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.

Also, C_ij = (–1)^i+j × M_ij

Given,

M₃₁ = 2×0 – 5×6

M₃₁ = –30

C₁₁ = (–1)¹⁺¹ × M₁₁

= 1 × 5

= 5

C₂₁ = (–1)²⁺¹ × M₂₁

= –1 × –40

= 40

C₃₁ = (–1)³⁺¹ × M₃₁

= 1 × –30

= –30

Now expanding along the first column we get

|A| = a₁₁ × C₁₁ + a₂₁× C₂₁+ a₃₁× C₃₁

= 0× 5 + 1 × 40 + 3× (–30)

= 0 + 40 – 90

= 50

(vi) Let M_ij and C_ij represents the minor and co–factor of an element, where i and j represent the row and column. The minor of matrix can be obtained for particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.

Also, C_ij = (–1)^i+j × M_ij

Given,

M₃₁ = h × f – b × g

M₃₁ = hf – bg

C₁₁ = (–1)¹⁺¹ × M₁₁

= 1 × (bc– f²)

= bc– f²

C₂₁ = (–1)²⁺¹ × M₂₁

= –1 × (hc – fg)

= fg – hc

C₃₁ = (–1)³⁺¹ × M₃₁

= 1 × (hf – bg)

= hf – bg

Now expanding along the first column we get

|A| = a₁₁ × C₁₁ + a₂₁× C₂₁+ a₃₁× C₃₁

= a× (bc– f²) + h× (fg – hc) + g× (hf – bg)

= abc– af² + hgf – h²c +ghf – bg²

(vii) Let M_ij and C_ij represents the minor and co–factor of an element, where i and j represent the row and column. The minor of matrix can be obtained for particular element by removing the row and column where the element is present. Then finding the absolute value of the matrix newly formed.

Also, C_ij = (–1)^i+j × M_ij

Given,

M₃₁ = –1(1 × 0 – 5 × (–2)) – 0(0 × 0 – (–1) × (–2)) + 1(0 × 5 – (–1) × 1)

M₃₁ = –9

M₄₁ = –1(1×1 – (–1) × (–2)) – 0(0 × 1 – 1 × (–2)) + 1(0 × (–1) – 1 × 1)

M₄₁ = 0

C₁₁ = (–1)¹⁺¹ × M₁₁

= 1 × (–9)

= –9

C₂₁ = (–1)²⁺¹ × M₂₁

= –1 × 9

= –9

C₃₁ = (–1)³⁺¹ × M₃₁

= 1 × –9

= –9

C₄₁ = (–1)⁴⁺¹ × M₄₁

= –1 × 0

= 0

Now expanding along the first column we get

|A| = a₁₁ × C₁₁ + a₂₁× C₂₁+ a₃₁× C₃₁ + a₄₁× C₄₁

= 2 × (–9) + (–3) × –9 + 1 × (–9) + 2 × 0

= – 18 + 27 –9

= 0

2. Evaluate the following determinants:

Solution:

(i) Given

⇒ |A| = x (5x + 1) – (–7) x

|A| = 5x² + 8x

(ii) Given

⇒ |A| = cos θ × cos θ – (–sin θ) x sin θ

|A| = cos²θ + sin²θ

We know that cos²θ + sin²θ = 1

|A| = 1

(iii) Given

⇒ |A| = cos15° × cos75° + sin15° x sin75°

We know that cos (A – B) = cos A cos B + Sin A sin B

By substituting this we get, |A| = cos (75 – 15)°

|A| = cos60°

|A| = 0.5

(iv) Given

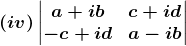
⇒ |A| = (a + ib) (a – ib) – (c + id) (–c + id)

= (a + ib) (a – ib) + (c + id) (c – id)

= a² – i² b² + c² – i² d²

We know that i² = -1

= a² – (–1) b² + c² – (–1) d²

= a² + b² + c² + d²

3. Evaluate:

Solution:

Since |AB|= |A||B|

= 2(17 × 12 – 5 × 20) – 3(13 × 12 – 5 × 15) + 7(13 × 20 – 15 × 17)

= 2 (204 – 100) – 3 (156 – 75) + 7 (260 – 255)

= 2×104 – 3×81 + 7×5

= 208 – 243 +35

= 0

Now |A|² = |A|×|A|

|A|²= 0

4. Show that

Solution:

Given

Let the given determinant as A

Using sin (A+B) = sin A × cos B + cos A × sin B

⇒ |A| = sin 10° × cos 80° + cos 10° x sin 80°

|A| = sin (10 + 80)°

|A| = sin90°

|A| = 1

Hence Proved

= 2(1 × 1 – 4 × (–2)) – 3(7 × 1 – (–2) × (–3)) – 5(7 × 4 – 1 × (–3))

= 2(1 + 8) – 3(7 – 6) – 5(28 + 3)

= 2 × 9 – 3 × 1 – 5 × 31

= 18 – 3 – 155

= –140

Now by expanding along the second column

= 2(1 × 1 – 4 × (–2)) – 7(3 × 1 – 4 × (–5)) – 3(3 × (–2) – 1 × (–5))

= 2 (1 + 8) – 7 (3 + 20) – 3 (–6 + 5)

= 2 × 9 – 7 × 23 – 3 × (–1)

= 18 – 161 +3

= –140

Solution:

Given

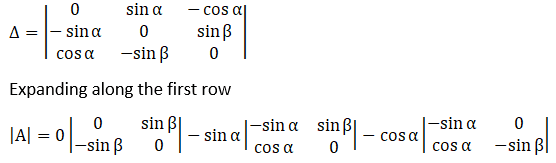
⇒ |A| = 0 (0 – sinβ (–sinβ)) –sinα (–sinα × 0 – sinβ cosα) – cosα ((–sinα) (–sinβ) – 0 × cosα)

|A| = 0 + sinα sinβ cosα – cosα sinα sinβ

|A| = 0

We have provided complete details of RD Sharma Solutions Class 12 Maths Chapter 6 Exercise 6.1. If you have any queries related to CBSE Class 12 Exam, feel free to ask us in the comment section below.

FAQs on RD Sharma Solutions Class 12 Maths Chapter 6 Exercise 6.1