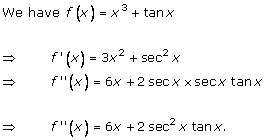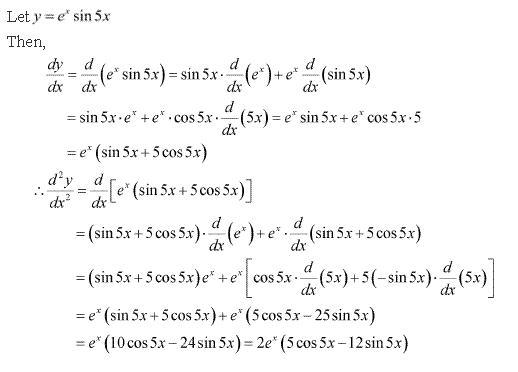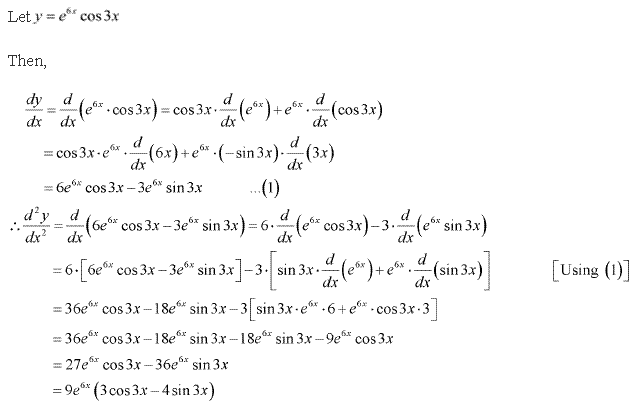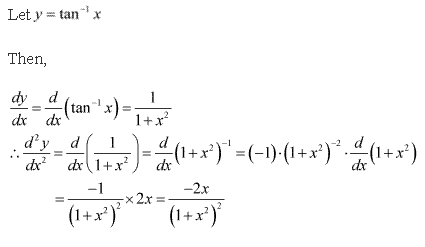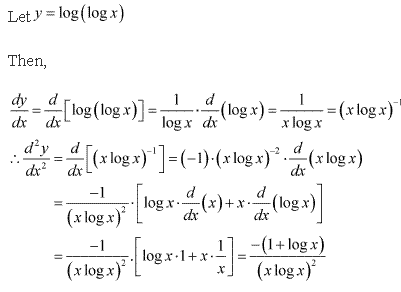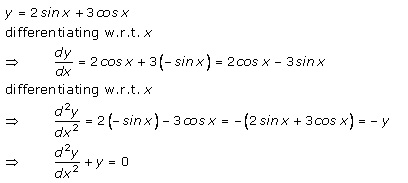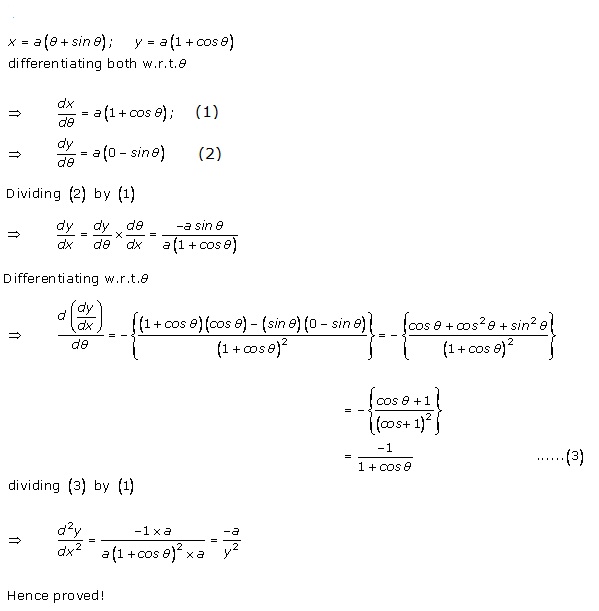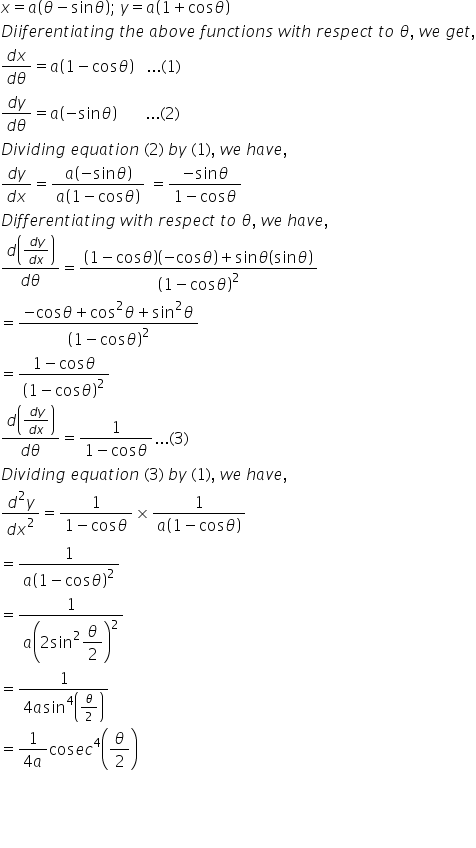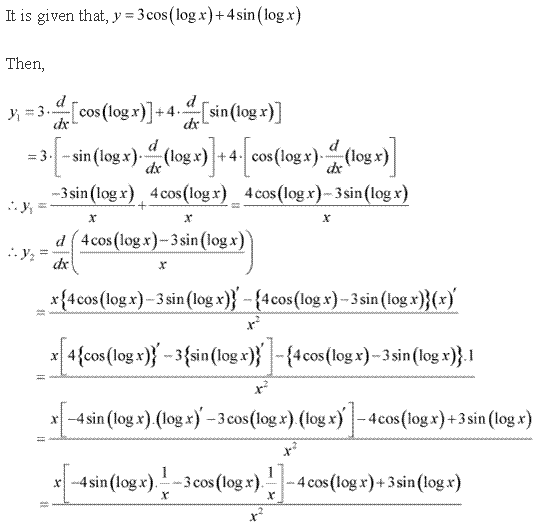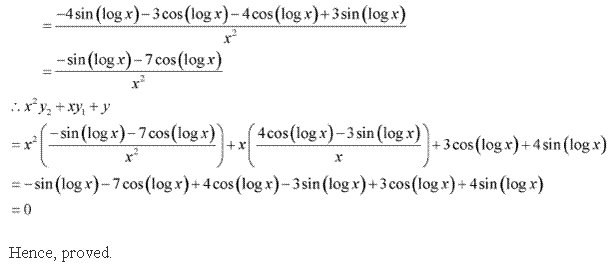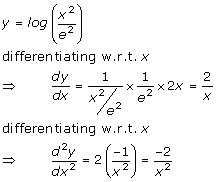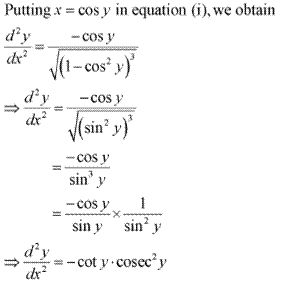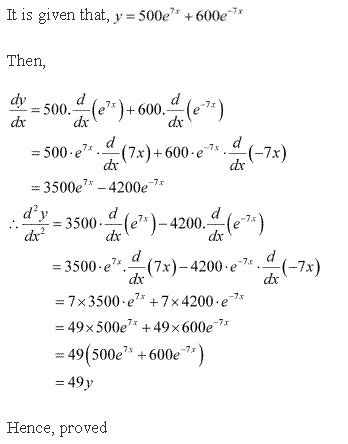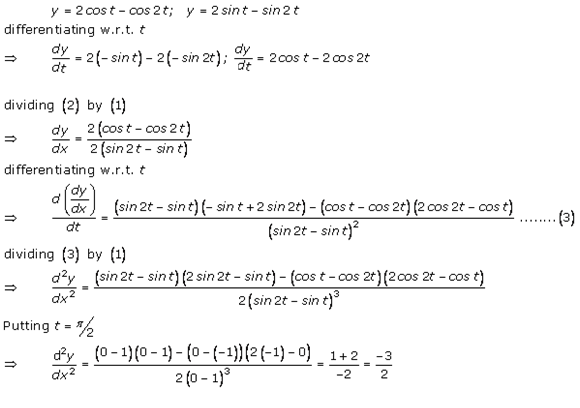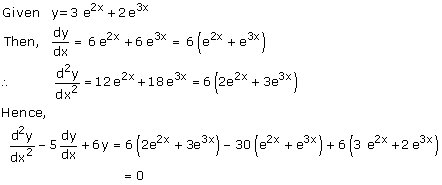RD Sharma Solutions Class 12 Maths Chapter 12 Exercise 12.1: The RD Sharma Class 12 Solutions Chapter 12 Exercise 12.1 is developed by math experts at Kopykitab to provide precise exercise-by-exercise solutions. These solutions also provide tips and tactics for rapidly and confidently solving complex questions. Students will be thorough with the topics offered in the RD Sharma textbook for Class 12 if they practice RD Sharma Solutions for Class 12 on a regular basis. Students can use the links below to download RD Sharma Solutions for Class 12 Maths Chapter 12 Exercise 12.1.
Download RD Sharma Solutions Class 12 Maths Chapter 12 Exercise 12.1 Free PDF
RD Sharma Solutions Class 12 Maths Chapter 12 Exercise 12.1
Access answers to Maths RD Sharma Solutions For Class 12 Chapter 12 – Higher Order Derivatives Exercise 12.1 Important Questions With Solution
1. Find the second-order derivatives of each of the following functions:
(i) x3 + tan x
Solution:
(ii) Sin (log x)
Solution:
(iii) Log (sin x)
Solution:
(iv) ex sin 5x
Solution:
(v) e6x cos 3x
Solution:
(vi) x3 log x
Solution:
(vii) tan-1x
Solution:
(viii) x cos x
Solution:
(ix) Log (log x)
Solution:
Higher Order Derivatives Ex 12.1 Q2
Higher Order Derivatives Ex 12.1 Q3
Higher Order Derivatives Ex 12.1 Q4
Higher Order Derivatives Ex 12.1 Q5
Higher Order Derivatives Ex 12.1 Q6
Higher Order Derivatives Ex 12.1 Q7
Higher Order Derivatives Ex 12.1 Q8
Higher Order Derivatives Ex 12.1 Q9
Higher Order Derivatives Ex 12.1 Q10
Higher Order Derivatives Ex 12.1 Q11
Higher Order Derivatives Ex 12.1 Q12
Higher Order Derivatives Ex 12.1 Q13
Higher Order Derivatives Ex 12.1 Q14
Higher Order Derivatives Ex 12.1 Q15
Higher Order Derivatives Ex 12.1 Q17
Higher Order Derivatives Ex 12.1 Q18
Higher Order Derivatives Ex 12.1 Q19
Higher Order Derivatives Ex 12.1 Q20
Higher Order Derivatives Ex 12.1 Q21
Higher Order Derivatives Ex 12.1 Q22
Higher Order Derivatives Ex 12.1 Q23
Higher Order Derivatives Ex 12.1 Q24
Higher Order Derivatives Ex 12.1 Q25
Higher Order Derivatives Ex 12.1 Q26
Higher Order Derivatives Ex 12.1 Q27
Higher Order Derivatives Ex 12.1 Q28
Higher Order Derivatives Ex 12.1 Q29
Higher Order Derivatives Ex 12.1 Q30
Higher Order Derivatives Ex 12.1 Q31
Higher Order Derivatives Ex 12.1 Q32
Higher Order Derivatives Ex 12.1 Q33
Higher Order Derivatives Ex 12.1 Q34
Higher Order Derivatives Ex 12.1 Q35
Higher Order Derivatives Ex 12.1 Q36
Higher Order Derivatives Ex 12.1 Q37
Higher Order Derivatives Ex 12.1 Q38
Higher Order Derivatives Ex 12.1 Q39
Higher Order Derivatives Ex 12.1 Q40
Higher Order Derivatives Ex 12.1 Q41
Higher Order Derivatives Ex 12.1 Q42
Higher Order Derivatives Ex 12.1 Q43
Higher Order Derivatives Ex 12.1 Q44
Higher Order Derivatives Ex 12.1 Q45
Higher Order Derivatives Ex 12.1 Q46
Higher Order Derivatives Ex 12.1 Q47
Higher Order Derivatives Ex 12.1 Q48
Higher Order Derivatives Ex 12.1 Q49
Higher Order Derivatives Ex 12.1 Q50
Higher Order Derivatives Ex 12.1 Q51
Higher Order Derivatives Ex 12.1 Q52
We have provided complete details of RD Sharma Solutions for Class 12 Maths Chapter 12 Exercise 12.1. If you have any queries related to CBSE, feel free to ask us in the comment section below.
FAQs on RD Sharma Class 12 Solutions Chapter 12 Exercise 12.1
Where can I get RD Sharma Class 12 Maths Solutions Chapter 12 Exercise 12.1 Free PDF?
You can get RD Sharma Solutions Class 12 Maths Chapter 12 Exercise 12.1 Free PDF from the above article.
How many questions are there in RD Sharma Solutions Class 12 Maths Chapter 12 Exercise 12.1?
There are a total of 52 questions in RD Sharma Solutions Class 12 Maths Chapter 12 Exercise 12.1.
Which is the best guidebook for preparing for the Class 12 exam?
The best reference material for CBSE board exam preparation is RD Sharma Solutions for Class 12 Maths Chapter 12 Exercise 12.1. Every section’s questions have been framed and solved by subject experts. They would be able to effortlessly excel in their final exams if they studied from these books.