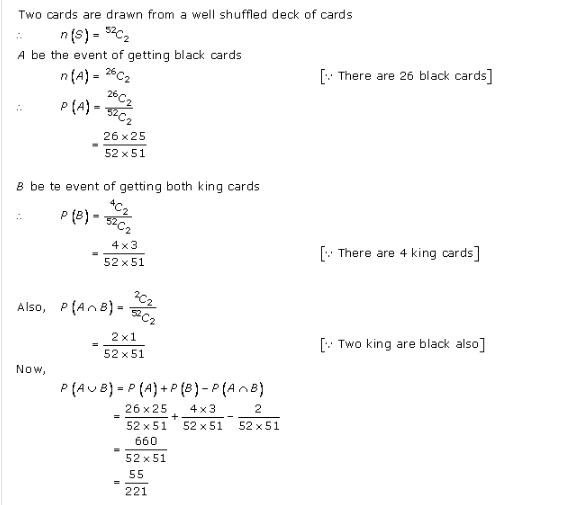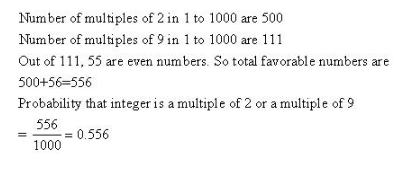RD Sharma Class 11 Solutions Chapter 33 Probability Exercise 33.4 (Updated for 2021-22)

RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.4: Until now, we’ve computed the likelihood of an event occurring or not occurring using the favourable and total number of elementary events. The RD Sharma Class 11 Solutions are described in simple language by topic experts to assist students in improving their analytical thinking and problem-solving abilities. RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.4 pdf can be downloaded for free to help students improve their exam preparation and score higher on their board exams.

Download RD Sharma Class 11 Solutions Chapter 33 Probability Exercise 33.4 Free PDF

RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.4

Access RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.4- Important Question with Answers

1. (a) If A and B be mutually exclusive events associated with a random experiment such that P (A) = 0.4 and P (B) = 0.5, then find:
(i) P(A ∪ B)

Solution:

Given: A and B are two mutually exclusive events.

P (A) = 0.4 and P (B) = 0.5

By definition of mutually exclusive events we know that:

P (A ∪ B) = P (A) + P (B)

Now, we have to find

(i) P (A ∪ B) = P (A) + P (B) = 0.5 + 0.4 = 0.9

(ii) P (A′ ∩ B′) = P (A ∪ B)′ {using De Morgan’s Law}

P (A′ ∩ B′) = 1 – P (A ∪ B)

= 1 – 0.9

= 0.1

(iii) P (A′ ∩ B) [This indicates only the part which is common with B and not A.

Hence this indicates only B]
P (only B) = P (B) – P (A ∩ B)

As A and B are mutually exclusive so they don’t have any common parts.

P (A ∩ B) = 0

∴ P (A′ ∩ B) = P (B) = 0.5

(iv) P (A ∩ B′) [This indicates only the part which is common with A and not B.

Hence this indicates only A]

P (only A) = P (A) – P (A ∩ B)

As A and B are mutually exclusive so they don’t have any common parts.

P (A ∩ B) = 0

∴ P (A ∩ B′) = P (A) = 0.4

(b) A and B are two events such that P (A) = 0.54, P (B) = 0.69 and P (A ∩ B) = 0.35. Find (i) P (A ∪ B)

Solution:

Given: A and B are two events.

P (A) = 0.54, P (B) = 0.69 and P (A ∩ B) = 0.35

By definition of P (A or B) under the axiomatic approach we know that:

P (A ∪ B) = P (A) + P (B) – P (A ∩ B)

Now we have to find:

(i) P (A ∪ B) = P (A) + P (B) – P (A ∩ B)

= 0.54 + 0.69 – 0.35

= 0.88

(ii) P (A′ ∩ B′) = P (A ∪ B)′ {using De Morgan’s Law}

P (A′ ∩ B′) = 1 – P (A ∪ B)

= 1 – 0.88

= 0.12

(iii) P (A ∩ B′) [This indicates only the part which is common with A and not B.

Hence this indicates only A]

P (only A) = P (A) – P (A ∩ B)

∴ P (A ∩ B′) = P (A) – P (A ∩ B)

= 0.54 – 0.35

= 0.19

(iv) P (A′ ∩ B) [This indicates only the part which is common with B and not A.

Hence this indicates only B]

P (only B) = P (B) – P (A ∩ B)

∴ P (A′ ∩ B) = P (B) – P (A ∩ B)

= 0.69 – 0.35

= 0.34

(c) Fill in the blanks in the following table:

Solution:

(i) By definition of P (A or B) under axiomatic approach we know that:

P (A ∪ B) = P (A) + P (B) – P (A ∩ B)

By using data from table, we get:

∴ P (A ∪ B) = 1/3 + 1/5 – 1/15

= 8/15 – 1/15

= 7/15

(ii) By definition of P (A or B) under axiomatic approach we know that:

P (A ∪ B) = P (A) + P (B) – P (A ∩ B)

P (B) = P (A ∪ B) + P (A ∩ B) – P (A)

By using data from table, we get:

∴ P (B) = 0.6 + 0.25 – 0.35

= 0.5

(iii) By definition of P (A or B) under axiomatic approach we know that:

P (A ∪ B) = P (A) + P (B) – P (A ∩ B)

P (A ∩ B) = P (B) + P (A) – P (A ∪ B)

By using data from table, we get:

∴ P (A ∩ B) = 0.5 + 0.35 – 0.7

= 0.15

Hence the table is:

2. If A and B are two events associated with a random experiment such that P (A) = 0.3, P (B) = 0.4 and P (A ∪ B) = 0.5, find P (A ∩ B).

Solution:

Given: A and B are two events.

P (A) = 0.3, P (B) = 0.5 and P (A ∪ B) = 0.5

Now we need to find P (A ∩ B).

By definition of P (A or B) under axiomatic approach (also called addition theorem) we know that:

P (A ∪ B) = P (A) + P (B) – P (A ∩ B)

So, P (A ∩ B) = P (A) + P (B) – P (A ∪ B)

P (A ∩ B) = 0.3 + 0.4 – 0.5

= 0.7 – 0.5

= 0.2

∴ P (A ∩ B) is 0.2

3. If A and B are two events associated with a random experiment such that P (A) = 0.5, P (B) = 0.3 and P (A ∩ B) = 0.2, find P (A ∪ B).

Solution:

Given: A and B are two events.

P (A) = 0.5, P (B) = 0.3 and P (A ∩ B) = 0.2

Now we need to find P (A ∪ B).

By definition of P (A or B) under axiomatic approach (also called addition theorem) we know that:

P (A ∪ B) = P (A) + P (B) – P (A ∩ B)

So, P (A ∪ B) = P (A) + P (B) – P (A ∩ B)

P (A ∪ B) = 0.5 + 0.3 – 0.2

= 0.8 – 0.2

= 0.6

∴ P (A ∪ B) is 0.6

Probability Ex 33.4 Q5

Probability Ex 33.4 Q6

Probability Ex 33.4 Q7

Probability Ex 33.4 Q8

Probability Ex 33.4 Q9

Probability Ex 33.4 Q10

Probability Ex 33.4 Q11

Probability Ex 33.4 Q12

Probability Ex 33.4 Q13

Probability Ex 33.4 Q14

Probability Ex 33.4 Q15

Probability Ex 33.4 Q16

Probability Ex 33.4 Q17

Probability Ex 33.4 Q18

Probability Ex 33.4 Q19

Probability Ex 33.4 Q20

Probability Ex 33.4 Q21

Probability Ex 33.4 Q22

Probability Ex 33.4 Q23

Probability Ex 33.4 Q24

Probability Ex 33.4 Q25

Probability Ex 33.4 Q26

Probability Ex 33.4 Q27

Probability Ex 33.4 Q28

We have provided complete details of RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.4. If you have any queries related to CBSE Class 11, feel free to ask us in the comment section below.

FAQs on RD Sharma Solutions Class 11 Maths Chapter 33 Exercise 33.4