RD Sharma Chapter 8 Class 9 Maths Exercise 8.3 Solutions is based on the vertically opposite angles this concerns under the Lines and Angles. The Vertically Opposite Angles are formed when the two lines cross. Vertical attributes to the Vertex, where they cross. With the help of this article, students will learn more about the Vertically Opposite Angles with illustrations, the theorem, and the proof.
The PDF attached to this article is prepared by our experts. The questions are solved with tricks and shortcuts. Also, the tips to solve the questions are mentioned with the solutions to the problems. Students get to solve the various questions of RD Sharma Chapter 8 Class 9 Maths Exercise 8.3 Solutions. Learners can download the PDF and do the practice for the exam by these problems, which are available with the solutions.
Download RD Sharma Chapter 8 Class 9 Maths Exercise 8.3 Solutions PDF
Solutions for Class 9 Maths Chapter 8 Lines and Angles Exercise 8.3
Important Definition RD Sharma Chapter 8 Class 9 Maths Exercise 8.3 Solutions
As we discussed above, the vertical angles are set when two lines meet each other at a point. There are two vertical angles, which are opposite to each other after the intersection of two lines.
A pair of vertically opposite angles are perpetually equal to each other. Also, a vertical angle and its adjacent angle are supplementary angles, i.e., they sum to 180 degrees. For example, if two lines intersect and form an angle, say A=45°, its opposite angle is equivalent to 45°. And the angle adjacent to angle A is equivalent to 180 – 45 = 135°.
Examples Related to the RD Sharma Chapter 8 Class 9 Maths Exercise 8.3 Solutions
Ques 1- In the given figure, find the measure of unknown angles.
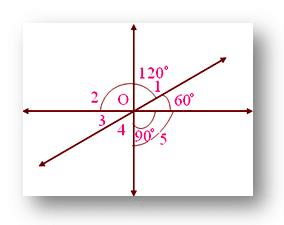
- ∠3= 60° vertically opposite angles
- ∠2 = 90° vertically opposite angles
- ∠2 + ∠1 + 60° = 180° (straight angle), 90° + ∠ 1 + 60° = 180°, 150° + ∠ 1 = 180° ∠1 = 180° — 150° = 30°
- ∠1 = ∠4 vertically opposite angles. So, ∠4 = 30°
Ques 2- If p = 30 degrees (30°) is a vertical angle when two lines intersect. Find all the angles?
Solution-
Given, vertical angle, p = 30
Let y is the angle vertically opposite to p, then q = 30 degrees (30°)
Now, as we know, vertical angle and its adjacent angle sum 180° (180 degrees)
So, the other two angles are- 180° – 30° = 150° (150 degrees).
Frequently Asked Questions (FAQs) of RD Sharma Chapter 8 Class 9 Maths Exercise 8.3 Solutions
Ques 1- How to measure vertical angles?
Ans- If the angle next to the vertical angle is provided to us, we can deduct it from 180° to get the vertical angle pattern because the vertical angle and its adjacent angle are supplementary to each other.
Ques 2- Are vertical angles equal to each other?
Ans- Vertical angles are perpetually equal to one another. The two pairs of vertical angles are set when two lines intersect.
Ques 3- Why are vertically opposite angles equal?
Ans- When two lines intersect, they set two pairs of opposite angles, P + R and Q + S. Another name for opposite angles is vertical angles. Vertical angles are evermore congruent, which means they are equivalent. Adjacent angles come out of the same vertex.
Ques 4- Can two vertical angles be supplementary?
Ans- Yes, two vertical angles can be supplementary, but only in definite cases. Supplementary angles have measures that sum up to 180°.
Ques 5- Can vertical angles be 90 degrees?
Ans- Vertical angles are opposite each other when two lines meet. The two pairs of opposite angles are equivalent to each other. The two pairs of adjacent angles are supplementary, meaning they sum up to 180°. Complementary angles are two angles that sum up to 90° (90 degrees).
