RD Sharma Chapter 10 Class 9 Maths Exercise 10.6 Solutions

RD Sharma Chapter 10 Class 9 Maths Exercise 10.6 Solutions: As we have learned that if two sides of a triangle are equivalent to the angles opposite to them, they are also similar and vice-versa. In this RD Sharma Chapter 10 Class 9 Maths Exercise 10.6 Solutions, we will learn about Some Inequality Relations in a Triangle.

This topic is mainly concerned with the RHS (Right angle-Hypotenuse-Side) and its concept. According to the Inequality Relations in a Triangle, the total of two sides of a triangle is perpetually greater than the third side of a triangle. Through this exercise, students will get a stepwise explanation of each problem with an example.

Furthermore, the PDF attached below helps students practice more with the variety of problems available. The questions are prepared by our experts using RD Sharma, the Previous Year’s Question Paper, and Text Book of Class 9.

Learn about RD Sharma Class 9 Chapter 10 (Congruent Triangles)

Download RD Sharma Chapter 10 Class 9 Maths Exercise 10.6 Solutions PDF

Solutions for Class 9 Maths Chapter 10 Congruent Triangles Exercise 10.6

Important Definitions RD Sharma Chapter 10 Class 9 Maths Exercise 10.6 Solutions

According to the theorem of Inequality Relations in a Triangle, for any triangle, the sum of two sides of a triangle is perpetually greater than the third side.

• A polygon surrounded by three line segments is called the Triangle. It is the least possible polygon.
• The triangle has three vertices, three sides, and three interior angles.
• The kinds of triangles are based on their angle measure and the length of the sides.
• The inequality theorem is appropriate for all triangles, such as isosceles triangles, equilateral triangles, and scalene triangles.

Proof of Theorem of Triangle Inequality

The theorem defines the relationship among the three sides of the triangle. According to this theorem, in any triangle, the total lengths of two sides are perpetually greater than the third side of a triangle. In simpler words, it defines that the smallest distance between two different points is always a straight line.

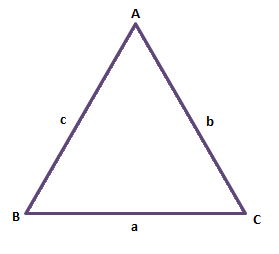
Suppose an ∆ABC as shown below, with a, b, and c as the side lengths.

The triangle inequality theorem declares that-

• a < b + c
• b < a + c
• c < a + b

Any triangle that has the least distance from any vertex to the opposite side is Perpendicular. In the figure below, XP is the least line segment from vertex X to side YZ.

Let’s prove the theorem now for a triangle ABC.

To Prove- |BC|< |AB| + |AC|

Construction: Suppose an ∆ABC. Increase the side AC to point D so that AD = AB, as shown in the following figure.

Statement	Reason
|CD|= |AC| + |AD|	From figure 3
|CD|= |AC| + |AB|	AB = AD, ∆ADB is an isosceles triangle
∠DBA <∠DBC	Since ∠DBC = ∠DBA+∠ABD
∠ADB<∠DBC	∆ADB is an isosceles triangle and ∠ADB = ∠DBA
|BC|<|CD|	The side opposite to the greater angle is a larger
|BC|<|AC| + |AB|	From statements 3 and 4

It concludes that the total of two sides of the triangle is greater than the third side.

Examples of RD Sharma Chapter 10 Class 9 Maths Exercise 10.6 Solutions

Ques: Could a triangle have side lengths as 6cm, 7cm, and 5cm?

Solution- If 6cm, 7cm, and 5cm are the sides of a triangle, it satisfies the inequality theorem.

Hence,

• 6 + 7 > 5 = 13 > 5 = True
• 7 + 5 > 6 = 12 > 6 = True
• 6 + 5 > 7 = 11 > 7 = True

All three conditions are satisfied. Therefore a triangle could have side lengths as 6cm, 7cm, and 5cm.

Ques- Is it possible to draw a triangle with sides of lengths- 2 cm, 3 cm, and 7 cm?

Solution-

Lengths of the sides are 2 cm, 3 cm, and 7 cm.

A triangle can be drawn only when the total of any two sides is greater than the third side.

So, let’s check the rule.

2 + 3 ≯ 7 or 2 + 3 < 7

2 + 7 > 3

and 3 + 7 > 2

Here 2 + 3 ≯ 7

So, the triangle does not exist.

Know about CBSE Board

FAQs on RD Sharma Chapter 10 Class 9 Maths Exercise 10.6 Solutions